The success of science, technological, and industrial developments are all directly proportional to making precise, accurate, and reliable measurements. For example, the product produced in the industry must be of high quality, sensitive, durable, and reliable. All these features can only be obtained by achieved by realizing high accuracy and precise measurement processes. When we express measured values, we can only list as many digits as we initially measured with our measuring tool (such as the rulers shown in Figure 1.24). For example, if you use a standard ruler to measure the length of a stick, you may measure it with a decimeter ruler as 3.6 cm. You could not express this value as 3.65 cm because your measuring tool was not precise enough to measure a hundredth of a centimeter.
Ask Any Financial Question
Similarly, 101 and 99 would be regarded as the same order of magnitude, 102. Order of magnitude can be thought of as a ballpark estimate for the scale of a value. The diameter of an atom is on the order of 10−9 m, while the diameter of the sun is on the order of 109 m. For example, the size of objects varies from something very small (like an atom) to something very large (like a star).
The Meter
The measurand is defined as the average thickness over the entire sheet in specified environmental conditions. This is the purest operational strategy and may be thought of as a refinement of Strategy 1, at the price of a complete lack of transferability of the information acquired in the process, which applies strictly only in the here-and-now conditions. The third black-box condition of measurement is that it requires an interaction with an object and that this interaction must be related to a property of that object, as depicted in Fig. The relations between language, knowledge, and the world, and more specifically between terms, concepts, and entities in the world, are effectively depicted in the so-called triangle of reference or semiotic triangle (Ogden & Richards, 1923), as in Fig.
Signed in but can’t access content
- The methods are ways of splitting the total joint costs between products.
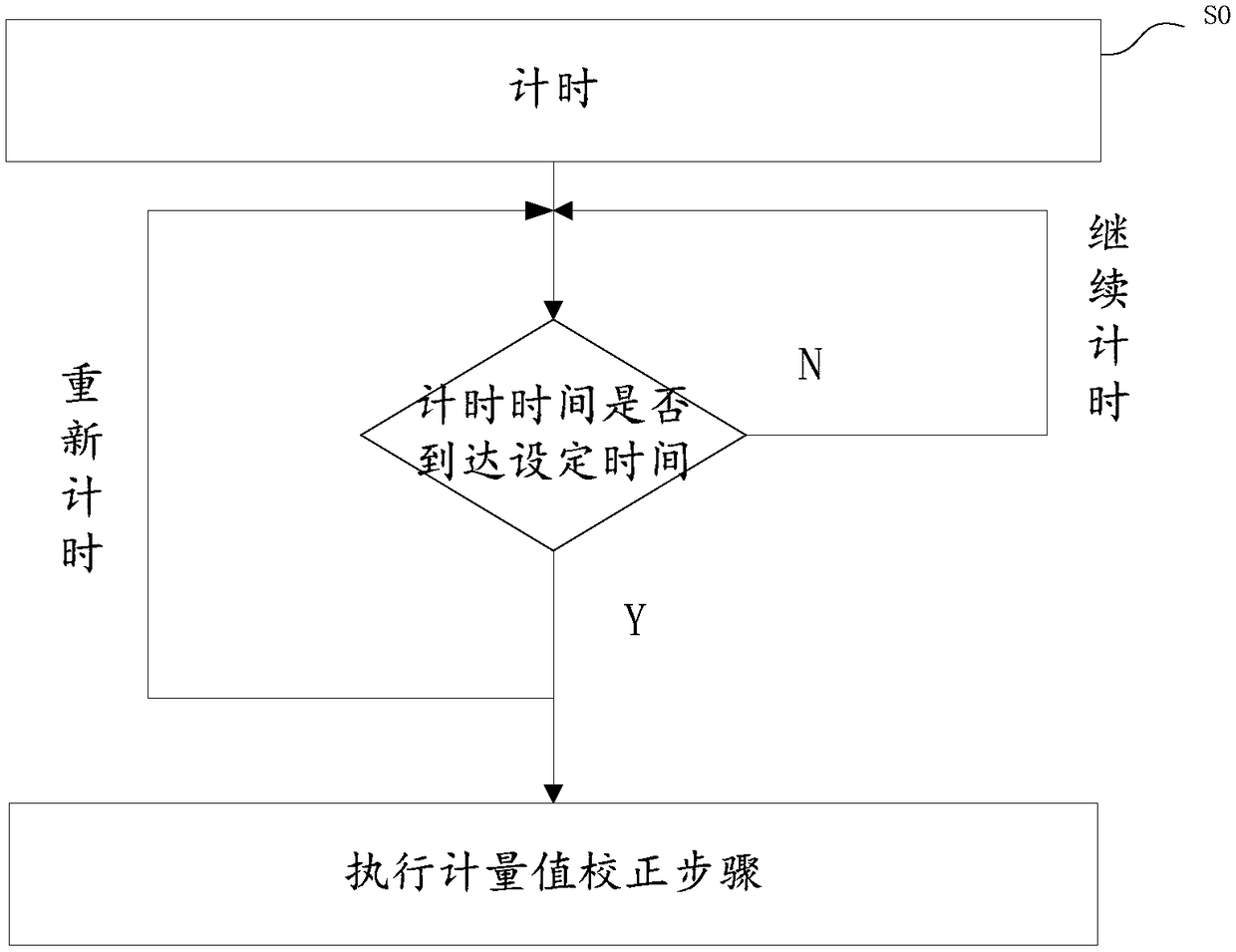
- When combining measurements with different degrees of accuracy and precision, the number of significant digits in the final answer can be no greater than the number of significant digits in the least precise measured value.
- Over the long duration of Egyptian history, the weight of the kite varied from period to period, ranging all the way from 4.5 to 29.9 grams (0.16 to 1.05 ounces).
- For that reason the elements, conditions, limitations, and theoretical foundations of measurement have been much studied.
This method is popular due to the argument that a product’s states with no income tax market value reflects the cost incurred to produce it.

Submit to get your question answered.
This tells you that you should move the decimal point 14 positions to the right, filling in placeholder zeros as you go. In this case, moving the decimal point 14 places creates only 13 placeholder zeros, indicating that the actual measurement value is 840,000,000,000,000. The metric system is convenient for scientific and engineering calculations because the units are categorized by factors of 10. Table 2 gives metric prefixes and symbols used to denote various factors of 10. The first thing to do is to list the units that you have and the units that you want to convert to. In this case, we have units in meters and we want to convert them to kilometers.
The sacred mina was equal to 60 shekels and the sacred talent to 3,000 shekels, or 50 sacred minas. The Talmudic mina equaled 25 shekels; the Talmudic talent equaled 1,500 shekels, or 60 Talmudic minas. The Babylonian liquid measure, qa (also spelled ka), was the volume of a cube of one handbreadth (about 99 to 102 millilitres or about 6.04 to 6.23 cubic inches). The cube, however, had to contain a weight of one great mina of water. The qa was a subdivision of two other units; 300 qa equaled 60 gin or 1 gur. The gur represented a volume of almost 303 litres (80 U.S. gallons).
Significant figures indicate the precision of a measuring tool that was used to measure a value. The measurements of physical quantities are expressed in terms of units, which are standardized values. For example, the length of a race, which is a physical quantity, can be expressed in meters (for sprinters) or kilometers (for long distance runners).
An important factor in the accuracy and precision of measurements is the precision of the measuring tool. In general, a precise measuring tool is one that can measure values in very small increments. A standard ruler can measure thickness to the nearest millimeter, while a micrometer can measure the thickness to the nearest 0.005 millimeter.
Over the long duration of Egyptian history, the weight of the kite varied from period to period, ranging all the way from 4.5 to 29.9 grams (0.16 to 1.05 ounces). Approximately 3,500 different weights have been recovered from ancient Egypt, some in basic geometric shapes, others in human and animal forms. Measurement theory dates back to the 4th century bc, when a theory of magnitudes developed by the Greek mathematicians Eudoxus of Cnidus and Thaeatetus was included in Euclid’s Elements. The first systematic work on observational error was produced by the English mathematician Thomas Simpson in 1757, but the fundamental work on error theory was done by two 18th-century French astronomers, Joseph-Louis Lagrange and Pierre-Simon Laplace. The first attempt to incorporate measurement theory into the social sciences also occurred in the 18th century, when Jeremy Bentham, a British utilitarian moralist, attempted to create a theory for the measurement of value. One important type of measurement is the analysis of resonance, or the frequency of variation within a physical system.



